ENTENDENDO O LSTM

Escrito por:

Diego Oliveira

Irei explicar o funcionamento de uma rede neural LSTM, sigla para Long Short-Term Memory, ou seja, uma memória de longo prazo. De início precisamos entender o que é uma rede neural artificial, para em seguida, entender o que é uma rede LSTM. E então, vamos nessa?

O QUE É UMA REDE NEURAL ARTIFICIAL (RNA)?

Uma Rede Neural Artificial (RNA) é uma técnica computacional inspirada na estrutura neural de organismos inteligentes, exemplo, celulas neurais do cérebro humano. Assim como as células neurais, essa técnica tem como objetivo “adquirir conhecimento” através da experiência. Na rede neural artificial é aplicado a regra da cadeia para atualizar os pesos da última camada e calcular a derivada dos parâmetros até a primeira camada.

No entanto, na rede neural simples existe um problema, que é a dependência de longo prazo durante a retropropagação, ou seja, ela tem problemas para armazenar informações de longo prazo. Uma solução para isso são as redes neurais LSTM (Long Short-Term Memory).

Long Short-Term Memory (LSTM)

Em uma arquitetura LSTM, a rede possue três entradas e retorna três saídas. A estrutura do LSTM possue três “portões”, que são o do Forget gate (portão do esquecimento), Input gate and output gate(portão de entrada e saída) e, por fim, o cell state (estado da célula). A imagem a seguir mostra como é uma célula de uma rede neural LSTM.

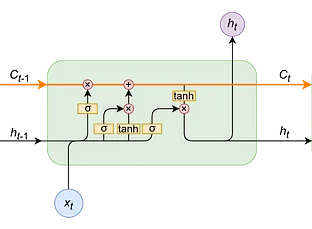
Célula LSTM

Forget gate

No portão do esquecimento é onde se decide quais informações devem ser lembradas ou esquecidas do estado anterior. A célula possue duas entradas, onde uma possue a informação do estado anterior, descrita como (ht -1) e a outra informação do estado atual, definida como (X(t)). Ambas são passadas pela função sigmóid, mas o que é uma função sigmóid? A função sigmóid é uma função matemática e seu nome advém do S do seu gráfico, como pode ser visto a seguir.

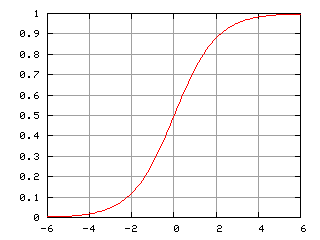
Função Sigmóid

O gráfico da função sigmóid pode ser obtida através da seguinte equação:

Equação da função Sigmóid

O valor de saída da função sigmóid estão entre 0 (zero) e 1 (um). Quanto mais próximo do valor 0 (zero) significa que será “esquecido” e quanto mais próximo do valor 1 (um) significa que será guardado a informação. Para tornar mais fácil o entendimento, basta verificar a imagem a seguir.

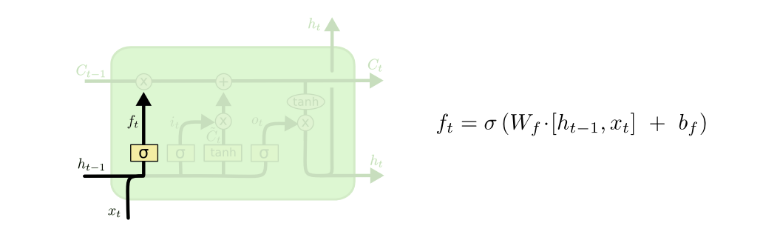
Forget gate (portão do esquecimento)

É possível verificar a equação utilizada para o cálculo do valor da função no portão do esquecimento, Onde;

Wf é a matriz de peso associado ao estado oculto
ht -1 é a informação do estado anterior
Xt é a informação do estado atual
bf é o peso associado do valor de entrada

Em seguida, é aplicado uma função sigmóide. Fazendo com que o valor obtido por ft seja um número entre 0 e 1.

Input gate

A porta de entrada é responsável pela divisão das informações importantes que devem ser adicionadas ao estado da célula com base nas entradas anteriores. Para atualizar o estado da célula é necessário passar o estado oculto anterior (h(t-1)) e a entrada atual dada por (x(t)) através da função sigmóid. Isso faz com que seja decidido quais valores serão atualizados, transformando os valores entre 0 (zero) e 1 (um). 0 (Zero) significa não importante e 1 (um) significa importante. Além disso, é passado a função oculta (h(t-1)) e a entrada atual (x(t)) para a função tangente hiperbólica (tanh) para “esmagar” valores entre -1 e 1, ajudando a regular a rede. Mas o que é uma função tangente hiperbólica?

A função tangente hiperbólica é uma função hiperbólica. Ela é obtida através da razão entre o seno hiperbólico e o cosseno hiperbólico, de forma similar à relação trigonométrica da tangente. A sua equação é a seguinte.

Equação tangente hiperbólico

Através dessa equação é possível obter a função da tangente hiperbólica no gráfico. Como é possível ver através da imagem a seguir.

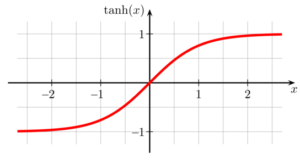
Gráfico tangente hiperbólico

Em seguida é multiplicada a saída da função tangente hiperbólico pela saída da função sigmóid. A saída sigmóid decidirá qual informação é importante manter da saída da função da tangente hiperbólica. A imagem a seguir mostra de maneira ilustrativa como é o Input gate (portão de entrada).

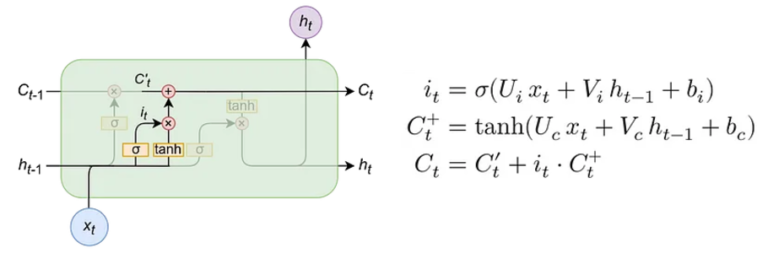
Input gate (portão de entrada)

Na imagem é possível verificar as equações utilizadas no input gate, onde cada símbolo significa o seguinte;

σ o símbolo sigma é a função sigmóid.
ht -1 é a informação do estado anterior
Xt é a informação do estado atual
Ui é o peso da matriz de entrada.
Vi é a matriz do peso de entrada associado ao estado oculto
bi é o peso associado do valor de entrada

Já a função Ct+ é uma nova informação de função de estado oculto. A função tanh faz com que a nova informação fique entre 0 (zero) e 1 (um). Caso o valor de Ct+ seja negativo, a informação é substituida do estado da célula, e, se for positivo a informação é adicionada à célula estado atual. Entretanto Ct+ não será adicionado diretamente no estado atual da célula, para isso serve a função Ct que utiliza as equações descritas anteriormente.

Cell State

Inicialmente o estado da célula é multiplicado pelo forget gate, isso possibilita descartar valores no estado da célula multiplicado por valores próximos a zero. Posteriormente, pega a saída do input gate e realiza uma adição pontual que atualiza o estado da célula para novos valores que a rede considera relevante, possibilitando obter um novo estado da célula (C(t)).

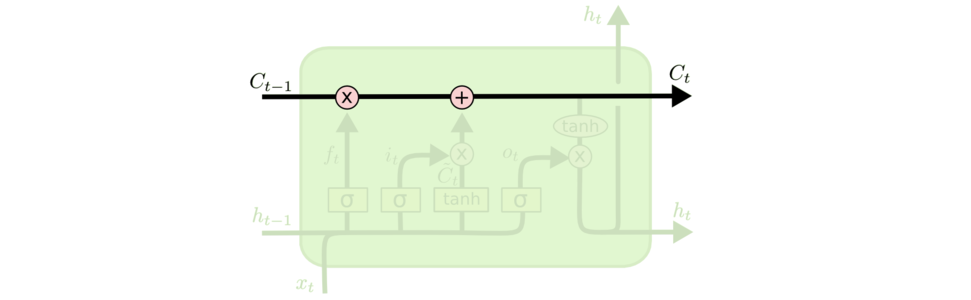
Cell State (estado da célula)

Output gate

O portão de saída decide qual o próximo estado oculto. O estado oculto tem informações dos estados anteriores, também usado para previsões. Primeiro o estado oculto e a entrada atual por uma função sigmóid, posteriormente passa o resultado por uma função tangente hiperbólica, multiplicando a saída da tangente hiperbólica pela a saída da função sigmóid para decidir quais informações o estado oculto deve transportar. A saída é o estado oculto. O novo estado da célula eo novo estado oculto são então transportados para a próxima etapa de tempo.

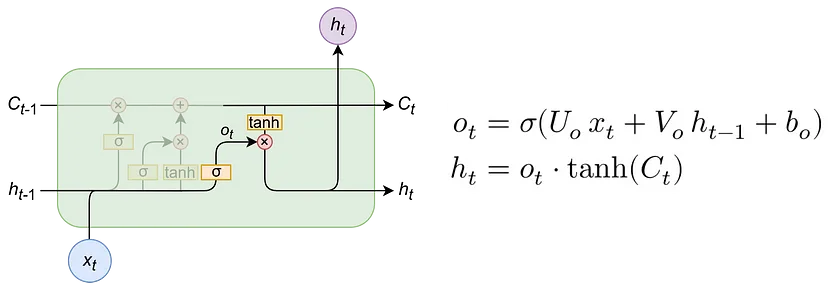
Output gate (portão de saída)

Na imagem é possível verificar as equações utilizadas no Output gate, onde cada símbolo significa o seguinte;

σ o símbolo sigma é a função sigmóid.
Ot significa Output gate
ht -1 é a informação do estado anterior
Uo é o peso da matriz de entrada do output.
Vo é a matriz do peso de entrada associado ao estado oculto do output
bo é o peso associado do valor de entrada do output
ht é o resultado final que significa a informação do estado atual.

Possíveis aplicações

O uso de redes neurais LSTM’s podem ser utilizadas para diversas soluções e aplicações, alguns exemplos destes são;

Geração de texto.
Reconhecimento de escrita.
Predição de séries temporais.
Aplicações para sistemas embarcados.

O uso de redes LSTM’s pode ser aplicado em diversas linguagens de programação, não existe a melhor linguagem, existe aquela que se adequa melhor no uso da aplicação, ou seja, a linguagem depende da aplicação que será realizada, exemplo, para séries temporais a linguagem de programação Python é mais adequada, pois já possuem diversas bibliotecas que facilitam a sua aplicação, mas se forem em outras aplicações como em sistemas embarcados, o ideal é utilizar a linguagem C ou C++.

Fontes:

Livro Mãos à obra: Aprendizado de Máquina com Scikit-Learn & TensorFlow

https://medium.com/turing-talks/turing-talks-27-modelos-de-predi%C3%A7%C3%A3o-lstm-df85d87ad210

https://towardsdatascience.com/illustrated-guide-to-lstms-and-gru-s-a-step-by-step-explanation-44e9eb85bf21

https://www.analyticsvidhya.com/blog/2021/03/introduction-to-long-short-term-memory-lstm/

Escrito por: